How to Draw Lattice Planes

Miller indices are ane of the most not-intuitive concepts well-nigh people encounter in an introductory course. And, since a few notation differences can completely alter the meaning, advanced students likewise come up back to review Miller Indices.

In this article, I'll explain what Miller indices are, why they're important, and how yous can read and write them. Avant-garde students can skip directly to the Review if they're just looking for a quick refresher.

Miller Indices are a iii-dimensional coordinate system for crystals, based on the unit prison cell. This coordinate system tin can bespeak directions or planes, and are ofttimes written as (hkl). Some mutual examples of Miller Indices on a cube include [111], the body diagonal; [110], the face diagonal; and (100), the face plane.

By the time you finish this commodity, you'll know what those numbers and symbols mean!

Basic Notation

The first supposition of Miller Indices is that yous know the crystal family. If yous don't know what crystals are, this topic volition exist super disruptive–you might want to check out this article starting time. If you lot're not sure well-nigh the unlike crystal families, yous tin read an explanation in this commodity nigh Bravais Lattices, but every bit long every bit y'all know what a "cube" is, you can understand Miller Indices.

Every crystal tin can be depicted as a hexahedron (that means it has 6 faces, like a cube). In that location are some crystallographic coordinate systems which have "extra" dimensions, like the (hkil) Miller-Bravais organisation for hexagonal crystals, but you can always reduce a conventional crystal jail cell into a primitive prison cell which is easily described by the (hkl) Miller Indices.

This article will continue with the traditional Miller Indices.

Miller Indices are a coordinate system (like the cartesian or polar coordinate systems you learned in high school), and so the first thing you need is an origin.

The origin is the signal $(0,0,0)$ and you can define it anywhere in your crystal. In most cases, the dorsum left corner of the crystal is the near natural point to define the origin.

Yous besides demand a sense of scale. For miller indices, the scale is the size of the unit cell. In other words, the value "0" is the origin of one unit cell, and the value "1" is the origin for the next unit of measurement cell over.

Miller indices too have weird way of writing negatives. Allegedly this was developed to save space in quondam crystallography journals. Instead of writing negative ane every bit "-1," nosotros write it every bit " $\bar{1}$ " and pronounce it as "bar 1." If you lot saw $[0\bar{1}0]$ you would pronounce that like "the zero bar one zero direction."

Information technology'southward also important to remember that crystals are defined by their symmetry. That'due south why the pick of origin is arbitrary. In some cases, nosotros may want to distinguish betwixt a specific management, and all equivalent directions. We make this distinction with brackets.

Don't worry, these full general rules volition make sense when we apply them to the specific case of points, directions, and planes.

Crystallographic Coordinate System

Miller indices utilize a coordinate system which is very like to the cartesian coordinate organisation. The cartesian system is the regular 2d or 3D coordinate system you lot used in high school, which has iii perpendicular axes 10, y, and z.

If you want a review of the cartesian arrangement, click to aggrandize.

Imagine you lot had a box with a length of four, a width of 2, and a meridian of iii. Put the lesser left corner of the box at the origin of your cartesian 3D arrangement. What is the position of the top correct corner?

If yous followed this picture, yous can see that the top right corner of the box is at the point $(4, 2, 3)$ . Its position is 4 spaces along the X-axis, 2 spaces forth the Y-axis, and three spaces along the Z-axis.

By definition, the origin is at $(0, 0, 0)$ considering it is 0 spaces along each centrality.

The only thing that changes betwixt the crystallographic cartesian system and the version you learned in high schoolhouse is the axes orientation.

In high school, you lot probably saw the 10-axis travel to the correct, the Y-axis travel upwards, and the Z-axis wasn't shown, simply travelled out of the folio.

In crystallography, nosotros use the Z-axis much more than in loftier school math. A clearer way to depict these axes is to have the Ten axis travel towards you (down and left), the Y axis travel to the correct, and the Z-centrality travel upward.

Then the point $(1, 2, 3)$ would be 1 stride toward you, ii steps to the right, and 3 steps upward (NOT 1 pace right, 2 steps upward, and iii steps out of the folio).

The concluding matter to remember about crystallographic coordinates is that the X-, Y-, and Z-axes may not be perpendicular to each other. In the cartesian arrangement, they are always perpendicular. In a cubic crystallographic system, they are also perpendicular, because the cubic lattice parameters are perpendicular.

However, not all crystals have perpendicular lattice parameters. For instance, a hexagonal lattice has 2 lattice parameters that are 120º to each other, which are both perpendicular to the third lattice parameter.

Every bit you tin can see, the point $(1, 1, 1)$ looks a bit unlike depending whether y'all have a cubic or hexagonal crystal structure. It's impossible to discuss Miller Indices without knowing the underlying crystal structure.

Miller Indices for Points

Technically, Miller Indices don't exist for points–but materials scientists and crystallographers stand for points with an unnamed annotation organization that is very similar to Miller Indices, so I will explicate that here. The main notation is that you utilise parentheses () and commas. The way yous write them is exactly the way you write cartesian coordinates.

I've actually used this notation system before in the article, and I'1000 sure you understood, considering it's very intuitive. Yous just need to follow the basic rules–0 is at the origin, and 1 is the distance of 1 unit cell. We likewise utilize the letter "h," m," and "50" to designate the 3 dissimilar lattice parameters.

For instance, in the cubic system, the three lattice parameters have the same length and are all perpendicular to each other (this is the definition of cubic). So, for all cubic crystals, "h" is the length of the cube's edge in the x-direction. "k" is the length of the cube's edge in the y-management. "50" is the length of the cube in the z-direction.

The aforementioned rules apply even in noncubic cases, but since the vector's aren't perpendicular to each other, the terms "x-centrality, y-axis, and z-axis" don't really make sense.

The point $(1, 1, 1)$ will ever exist the acme right corner, opposite the origin. The betoken $(\frac{1}{2}, \frac{1}{2}, \frac{1}{2})$ will always be the center of the crystal.

Call up, when describing points you write the point as (h, k, l). You likewise use negative signs, rather than the "bar" notation. In other words, y'all write $(-h, -k, -l)$ instead of $(\bar{h}, \bar{k}, \bar{l})$ .

Miller Indices for Directions

To depict a direction, all you lot need to know is the point you desire to travel to, relative to the origin. For example, if you desire to travel to the right, the bespeak straight to the right of the origin $(0, 0, 0)$ is $(0, 1, 0)$ . All you lot demand to practise is take this indicate and properly format it.

If you remember, the format for directions is a foursquare subclass $[hkl]$ . If you lot wanted to talk about the family of directions, employ angle brackets $\langle hkl \rangle$ .

Then, to indicate the direction "correct" in a cubic crystal y'all would write $[010]$ . The direction "left" would be $[0\bar{1}0]$ .

The $[010]$ direction looks a fleck unlike in the hexagonal system, only information technology's still just the length and direction of the 2d lattice parameter. If you wanted to evidence a line to the "correct" in a hexagonal system (depending on where nosotros define the original axes), you would need to use a linear combination of ii lattice parameters. In other words, $[110]$ .

Finally, it's customary to reduce fractions. The "length" of the direction doesn't matter. If y'all wanted to indicate a direction that travels ¼ up the x-axis while going all the mode beyond the y-axis, information technology's traditional to write that as $[140]$ instead of $[\frac{1}{4}10]$ , by multiplying that latter version by four until everything is a whole number.

Miller Indices for Planes

Reading Miller indices for planes is a fleck different, because we have to enter "reciprocal infinite."

Reciprocal space means y'all take the inverse of whatever point you lot were thinking of. The changed of 1 is still 1, the inverse of 2 is ½, and the changed of 0 is infinity.

Here is the 3-step process to discover the miller indices for planes.

Detect the signal where the plane intersects each axis. If the plane never intersects an axis because it is parallel to that centrality, the intersection point is ∞.
Take the inverse of each intersection point.
Put those three values in the proper (hkl) format. Remember that negatives are expressed with a bar, parenthesis () betoken a specific plane, and curly brackets {} betoken the family unit of planes. Don't use any commas or spaces!

In a cubic system, information technology turns out that the direction $[hlk]$ will always be perpendicular to the aeroplane $(hkl)$ . For example the $[110]$ direction is perpendicular to the $(110)$ plane.

This is not necessarily truthful in non-cubic systems.

Directional Families

Directional families are the prepare of identical directions or planes. These families are identical because of symmetry.

Imagine that I handed you lot a cube and asked you to describe the $[100]$ . Past now, I promise you could do this easily! However, if I gave the same cube to someone else, they would probably draw a unlike $[100]$ , because they chose a different origin or a different initial rotation.

The line yous originally drew may look like $[001]$ compared to the other person'due south version of $[100]$ .

In this way, we can say that $[001]$ and $[100]$ belong to the same directional family. The only way to distinguish between the two is to define a consistent rotational frame of reference. This means that any material property which is true along $[100]$ will likewise be true of $[001]$ or any other direction in the $\langle 100 \rangle$ family.

To observe the different directional families, find all the permutations that can replace $[hkl]$ with a negative version, such as $[\bar{h}kl]$ or $[h\bar{k}\bar{l}]$ . If the lattice vectors are the same length and have the same angle betwixt them, you lot tin besides change the gild, such as $[klh]$ or $[hlk]$ .

Here is a list of the individual directions in the directional families $\langle 100 \rangle$ , $\langle 110 \rangle$ , $\langle 111 \rangle$ . If two directions belong to the same directional family, their corresponding planes will too belong to the aforementioned planar family unit.

Since the cubic lattice has the most symmetry, there are the virtually number of identical directions in each directional family. Imagine, however, that you lot had a tetragonal crystal that was longer in the $[100]$ direction than the $[001]$ direction. In this instance, they would Not vest to the same family. $[100]$ and $[010]$ would vest to the aforementioned family, which you could call $\langle 100 \rangle$ or $\langle 010 \rangle$ . However, the $\langle 001 \rangle$ family would only include $[001]$ and $[00\bar{1}]$ .

Identifying directional families becomes particularly confusing if the lattice parameters h, k, and l are not perpendicular to each other. This was the main motivation for creating Miller-Bravais indices, which only employ to hexagonal crystals and convert the 3-term (hkl) values into 4-term (hkil) values. This conversion is a fleck complex, merely allows you to place hexagonal directional families just based on the numerical value of the index.

Culling Notations

Avant-garde topic, click to expand.

This is going into collapsable text because it's an advanced topic, about different letters that may exist used to designate different axes or positions along the axes.

In this commodity, I've tried to use h, yard, and l, for the values inside the Miller Index, and x-axis, y-axis, and z-axis for the directions.

It'due south too common to use "U," "V," and "W" to designate directions, every bit in [UVW] vs (hkl).

Additionally, the way I used x-, y- and z-axes is technically incorrect. We're technically supposed to use the lattice vectors, rather than cartesian axes. In the cubic organisation, they are the same, but they are not the same in other crystal systems.

Lattice vectors are often described using the messages " $a$ ," " $b$ ," and " $c$ ." Sometimes yous might run across the latters " $a_1$ ," " $a_2$ ," and " $a_3$ ," although this notation is typically used only with archaic cells.

I have tried to write this article in a way that is nigh understandable for people trying to larn Miller Indices, but I think it'due south important to know that yous'll see modest notational differences in existent scientific journals or textbooks that talk over some theory of the indices. In virtually practical cases, you volition just need to sympathize the meaning of basic indices such as $[100]$ , $\langle 111 \rangle$ , $(220)$ , and $\{110\}$ .

Review

At present you know how to read and write Miller indices! For a quick review of notation:

(h, grand, fifty) is for points. Remember to use the negative sign (-h) instead of bar sign ( 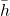$\bar{h}$ ) and don't reduce fractions–these rules use to directions and planes.
[hkl] is for a specific direction.
<hkl> is for a family of directions.
(hkl) is for a specific airplane. Retrieve most reciprocal (changed) space in planes!
{hkl} is for a family unit of planes.

Before you go, you may be interested in practicing a few instance problems.

Example Issues

Practice ane. Draw the $[100]$ , $[111]$ , and $[010]$ directions in a cubic crystal.

Click here to check out the solution!

Ascertain an origin. I'll choose the back left corner to define as my $(0, 0, 0)$ point
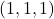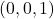Notice the corresponding $(1, 0, 0)$ , $(1, 1, 1)$ , and $(0, 0, 1)$ points because they take the same 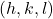$(h, k, l)$ values as the directions you want.
The line from the origin to these points, extending infinitely, is your direction.

Practise 2. Write the Miller Indices of the indicated direction.

Click hither to check out the solution!

Offset, define an origin. It'south ever okay to move the origin later, since crystals-by definition–repeat between unit cells. In this example, you need the origin to intersect along the indicated direction, so yous can move the origin the back left corner. Alternatively, you could simply translate that vector and so information technology intersects with the back-left corner.

Either way, y'all'll run across that information technology takes a movement of 0 unit cells in the ten-direction, 0 unit cells in the y-direction, and i unit prison cell in the z-direction to motion forth that vector. Thus, the management is $[001]$ .

Practise three. Write the position of the betoken, and the Miller Index for the direction from the origin to the point. Assume the origin is at the back left corner.

Click here to bank check out the solution!

Hopefully it's straightforward to find this indicate, especially since I labelled the position for you. Yous need to translate 1 unit jail cell in the ten-direction, ⅔ unit of measurement cell in the y-management, and ½ unit of measurement cell in the z-direction. Thus, the indicate is at location $( \frac{1}{2} ,\frac{2}{3}, \frac{1}{2})$ .

The direction would exist identical, except that we adopt to avert fractions. Recollect that directions extend infinitely, so nosotros can easily multiply the $( \frac{1}{2} ,\frac{2}{3}, \frac{1}{2})$ value by 6, which is a mutual denominator. Thus, the direction is really $[343]$ .

Practice 4. Draw the directions $[\bar{1}00]$ and $[010]$ , and write the Miller Alphabetize for the airplane common to both directions.

Click here to check out the solution!

Hmm…What should you do almost a negative value? Travel out of the unit of measurement cell? That's a perfectly valid process, considering in that location is an identical unit cell behind the original version. If yous notice, in that 2nd unit cell information technology looks like the vector comes out of the front-left corner.

Because at that place'southward e'er translational symmetry betwixt unit of measurement cells, you can freely define a convenient origin (such as the forepart-left corner), change your frame of reference to a dissimilar unit prison cell, or simply interpret the direction to stay within your current unit of measurement cell.

If nosotros draw both directions like this, it'south articulate that the airplane between them is the "basal" plane, or the flooring/roof (remember past translation, the floor of 1 unit prison cell is the roof of another).

To notice the airplane, we need to decide where it intersects with the lattice parameters.

This plane never intersects with the x-centrality or y-axis, because information technology is parallel to them. Thus, the h value is ∞ and the chiliad value is ∞. The plane intersects with the z-axis at betoken 0. By translation, 0 is also ane, so the 50 value is 1.
The reciprocal of ∞ and 1 is 0 and ane.
Thus, the (hkl) value of the plane is (001).
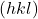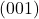Every bit a sanity check, recall that in cubic systems, the $[hkl]$ direction will exist perpendicular to the $(hkl)$ plane. Past now I hope it's like shooting fish in a barrel to draw the $[001]$ direction, which you can see is perpendicular to the $(001)$ plane.

Practise 5. Draw the $(220)$ and $(111)$ planes in a cubic crystal.

Click here to bank check out the solution!

By the reciprocal rule, the $(220)$ plane intersects the x-axis at ½, the y-centrality at ½, and never intersects the z-centrality. The $(110)$ plane intersects the x-axis at 1, the y-axis at i, and never intersects the z-axis. Nosotros can describe that like this.

Detect that the $(220)$ and $(110)$ are parallel, only not identical. If I had an cantlet at $(0, \frac{1}{2}, \frac{1}{2})$ it would intersect the $(220)$ plane but not $(110)$ plane. This distinction matters more if you do diffraction experiments.

Do 6. Draw the $[110]$ direction and $(110)$ plane in the hexagonal lattice.

Click here to check out the solution!

Let's outset identify the direction. Retrieve, the hexagonal lattice parameters are non perpendicular, but I'll keep calling them the x-, y-, and z-axes because that is more familiar for about of my readers.

The $[110]$ is one step in the x-direction and one pace in the y-direction, like so:

To find the plane, let's plot our intersection points. It will intersect the ten- and y-axes at the end of the unit jail cell (reciprocal of 1 is 1), and will exist parallel to the z-centrality (reciprocal of 0 is infinity).

References and Further Reading

If yous desire to bank check your work, you can find a "Miller Index aeroplane estimator" for cubic lattice from the University of Cambridge Dissemination of IT for the Promotion of Materials Science.

If you're reading this article as an introductory educatee in materials scientific discipline, welcome! I hope y'all can discover many other useful articles on this website. You may be interested in a related article I've written most Atomic Packing Gene.

If y'all're reading this article because you're taking a class on structures, you may be interested in my other crystallography articles. Here is this list, in recommended reading club:

Introduction to Bravais Lattices
What is the Divergence Between "Crystal Structure" and "Bravais Lattice"
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Shut-Packed Crystals and Stacking Lodge
Interstitial Sites
Archaic Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups

If y'all are interested in more details about any specific crystal structure, I have written individual manufactures about simple crystal structures which correspond to each of the 14 Bravais lattices:

1. Elementary Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
six. Simple Tetragonal
seven. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
eight. Simple Orthorhombic
9. Base of operations-Centered Orthorhombic
10. Confront-Centered Orthorhombic
xi. Trunk-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
fourteen. Triclinic

turnerciame1995.blogspot.com

Source: https://msestudent.com/miller-indices/

How to Draw Lattice Planes

Basic Notation

Crystallographic Coordinate System

Miller Indices for Points

Miller Indices for Directions

Miller Indices for Planes

Directional Families

Culling Notations

Review

Example Issues

References and Further Reading

0 Response to "How to Draw Lattice Planes"

Enregistrer un commentaire

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel